Es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y,cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

unidades angulares
- Radián: unidad angular natural en trigonometría. En una circunferencia completa hay 2π radianes (algo más de 6,28).
- Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
- Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.
- Mil angular: unidad angular que divide la circunferencia en 6400 unidades.
 |  |
| Transportador en radianes | Transportador en grados sexagesimales |
 | 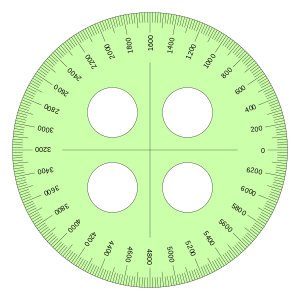 |
| Transportador en grados centesimales | Transportador en mil angular |
Razones trigonométricas
El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo  , correspondiente al vértice A, situado en el centro de la circunferencia.
, correspondiente al vértice A, situado en el centro de la circunferencia.
 , correspondiente al vértice A, situado en el centro de la circunferencia.
, correspondiente al vértice A, situado en el centro de la circunferencia.- El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.

- El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa.
- La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente.

- gráfica

representación
Razones trigonométricas inversas
- La cosecante: (abreviado como csc o cosec) es la razón inversa de seno, o también su inverso multiplicativo:
En el esquema su representación geométrica es:
- La secante: (abreviado como sec) es la razón inversa de coseno, o también su inverso multiplicativo:
En el esquema su representación geométrica es:
- La Cotangente: (abreviado como cot o cta o ctg) es la razón inversa de la tangente, o también su inverso multiplicativo:
En el esquema su representación geométrica es:
Representación gráfica

Funciones trigonométricas recíprocas
Las funciones recíproca se denominan con el prefijo arco, cada razón trigonométrica posee su propia función recíproca:
y es igual al seno de x, la función recíproca:
x es el arco cuyo seno vale y, o también x es el arcoseno de y.
si:
y es igual al coseno de x, la función recíproca:
x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.
si:
y es igual al tangente de x, la función recíproca:
x es el arco cuya tangente vale y, o x es igual al arcotangente de y.
NOTA: Es común, que las funciones recíprocas sean escritas de esta manera:
pero se debe tener cuidado de no confundirlas con:
Representación gráfica

EQUIVALENCIA ENTRE LAS FUNCIONES TRIGONOMÉTRICAS
| Seno | Coseno | Tangente | Cotangente | Secante | Cosecante | |
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  | 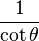 |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
VALOR DE LAS FUNCIONES TRIGONOMÉTRICAS
 |  |
| Circunferencia en radianes. | Circunferencia en grados sexagesimales. |
| Radianes | Grados sexagesimales | seno | coseno | tangente | cosecante | secante | cotangente | |
|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  | 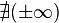 |  | 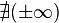 |
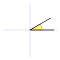 |  | 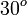 |  |  | 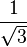 | 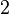 |  | 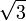 |
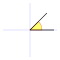 |  |  |  |  |  |  |  |  |
 | 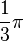 | 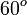 |  |  | 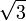 |  | 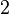 | 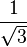 |
 |  |  |  |  | 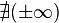 |  | 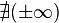 |  |
ANGULOS TRIGONOMETRIA
Definición y medida de ángulos: Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados del ángulo ,el origen común es el vértice.
Radianes
 Es la medida del ángulo central de una circunferencia cuya longitud de arco coincide con la longitud de su radio.
Es la medida del ángulo central de una circunferencia cuya longitud de arco coincide con la longitud de su radio.
Ángulos notables
Razones trigonométricas de 30º y 60º:
 La altura divide al triángulo equilátero en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 60º y 30º.
La altura divide al triángulo equilátero en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 60º y 30º.
Ángulo doble
Seno del ángulo doble


Coseno del ángulo doble


Tangente del ángulo doble


Teorema de los senos
Cada lado de un triángulo es directamente proporcional
al seno del ángulo opuesto.
Teorema del coseno
En un triángulo el cuadrado de cada lado es igual a la suma de
los cuadrados de los otros dos,menos el doble producto del producto
de ambos por el coseno del ángulo que forman.
Teorema de las tangentes

AQUI LES DEJO UN VIDEO PARA QUE SE INFORMEN MÁS .
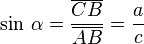
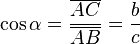

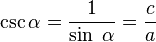
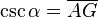
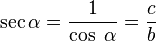
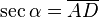

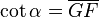
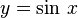

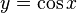

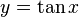









No hay comentarios.:
Publicar un comentario