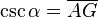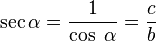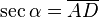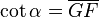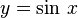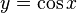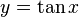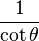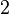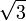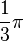la matematica es divertida : 2016

CUERPOS GEOMÉTRICOS

Los geométricos son figuras idealizadas de objetos de la vida real .Esos cuerpos físicos reales nos permiten construir el espacio geométrico . Los cuerpos geométricos , no tienen existencia en el espacio físico , existe en nuestra mente , entes abstractos .

puedes ver cómo es posible idealizar un objeto tan común como la lata .

CLASIFICACIÓN

Observa estos cuerpos geométricos. todos ellos están limitados por polígonos y se llaman poliedros, pero hay otros que conoceremos en páginas siguientes.

Poliedro es una porción de espacio limitadas por polígonos.

Algunos cuerpos tienen superficies no planas (todas o solo algunas ) así que no son poliedros.

POLIEDROS

Como ya vimos un poliedro es una porción de espacio limitada por polígonos .

Elementos de un poliedro :

Esta figura es un poliedro que está formado por dos caras que son pentágonos y cinco caras laterales que son paralelogramos.

Este poliedro se llama de base pentagonal .

Las caras de un poliedro , que son los polígonos que lo limitan.

Las aristas de un poliedro ,que son los lados de las caras.

Los vértices de un poliedro , que son los puntos donde se juntan tres o más aristas .

PRISMAS

Son los poliedros que están limitados por dos bases que son polígonos iguales y por las caras laterales que son paralelogramos .

Los prismas se nombran según el polígono de la base .

prisma triangular

prisma cuadrangular

prisma pentagonal

prisma hexagonal

PRISMAS RECTOS , OBLICUOS , REGULARES E IRREGULARES.

PIRÁMIDES

Los elementos fundamentales de una pirámide son caras , aristas y vértices .

LAS CARAS PUEDEN SER :

-Base de la pirámide , que es un polígono cualquiera .

-Caras laterales de la pirámide , que son triángulos .

LAS ARISTAS PUEDEN SER :

-Aristas básicas , que son los lados de la base .

-Aristas laterales, que son los las de las caras laterales que no son aristas básicas .

LOS VÉRTICES PUEDEN SER :

-Vértices de la base , que son los vertices del poligono de la base .

-Vértice o cúspide de la pirámide ,que es el punto en que se encuentran las aristas laterales .

-La altura es la distancia del vértice a la base .

POLIEDROS REGULARES

Cuyas caras son polígonos regulares iguales entre si y en cuyos vértices concurren el mismo número de caras .

Los prefijos tetra, Hexa , Octa , Dodeca e Icosa que dan nombre a los cinco poliedros regulares indican el número de polígonos (caras) que forman el cuerpo .

NO POLIEDROS

Dentro de los no poliedros veremos la esfera , el cono y el cilindro , llamados cuerpos de revolución porque pueden obtenerse a partir de una figura que gira alrededor de un eje .

Geometría

Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, politopos (que incluyen paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.). Sus orígenes se remontan a la solución de problemas concretos relativos a medidas. Tiene su aplicación práctica en física aplicada,mecánica, arquitectura, geografía, cartografía, astronomía, náutica, topografía, balística etc. Y es útil en la preparación de diseños e incluso en la elaboración de artesanía.

TIPOS DE GEOMETRÍA

Desde los antiguos griegos, ha existido numerosas contribuciones a la geometría, particularmente a partir del siglo XVIII. Eso ha hecho que proliferen numerosas subramas de la geometría con enfoques muy diferentes. Para clasificar los diferentes desarrollos de la Geometría moderna se pueden recurrir a diferentes enfoques:

La geometría absoluta , que es el conjunto de hechos geométricos derivables a partir únicamente de los primeros cuatro postulados de Euclides.
La geometría euclidiana , que es la geometría particular que se obtiene de aceptar como axioma también el quinto postulado. Los griegos consideraron dos variantes de geometría euclídea:
- Geometría euclídea del plano
- Geometría euclídea del espacio
La geometría clásica es una recopilación de resultados para las geometrías euclídeas.

A partir del siglo XIX se llegó a la conclusión de que podían definirse geometrías no euclídeas entre ellas:

GEOMETRÍA ASOCIADAS A TRANSFORMACIONES

En el siglo XIX se constató que otra forma de enfocar los conceptos geométricos era estudiar la invarianza de ciertas propiedades bajo diferentes tipos de transformaciones matemáticas, así se clasificaron diversas propiedades geométricas en grupos y se plantearon subdisciplinas consistentes en ver cuales eran las propiedades invariantes bajo tipos particulares de transformaciones, así aparecieron los siguientes tipos de enfoques geométricos:

GEOMETRÍA SEGÚN EL TIPO DE REPRESENTACIÓN

Si bien Euclides básicamente se restingió a conceptos geométricos representables mediante figuras (puntos, líneas, círculos, etc.)

-La geometría algebraica

-La geometría analítica
-La geometría descriptiva
-La Topología geométrica

-La geometría diferencial que engloba como ramas a:
Geometría diferencial discreta
-La geometría de curvas y superficies

-La Geometría diferencial de curvas
-La Geometría diferencial de superficies
-La Geometría diferencial de hipersuperficies

-Geometría diferencial de variedades

-La geometría de Riemann
-La Geometría fractal

-Geometría sintética

TRIGONOMETRÍA

Es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y,cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Representación gráfica de un triángulo rectángulo en un sistema de coordenada cartesiana

unidades angulares

Radián: unidad angular natural en trigonometría. En una circunferencia completa hay 2π radianes (algo más de 6,28).
Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.
Mil angular: unidad angular que divide la circunferencia en 6400 unidades.


Transportador en radianes	Transportador en grados sexagesimales

Transportador en grados centesimales	Transportador en mil angular

Razones trigonométricas

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo $\alpha \,$ , correspondiente al vértice A, situado en el centro de la circunferencia.

El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.

$\sin \, \alpha = \frac{\overline{CB}}{\overline{AB}} = \frac{a}{c}$

El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa.

$\cos\alpha = \frac{\overline{AC}}{\overline{AB}} = \frac{b}{c}$

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente.

$\tan\alpha = \frac{\overline{CB}}{\overline{AC}} = \frac{a}{b}$

representación

gráfica

Razones trigonométricas inversas

La cosecante: (abreviado como csc o cosec) es la razón inversa de seno, o también su inverso multiplicativo:

\csc \alpha = \frac{1}{\sin \; \alpha} = \frac{c}{a}

En el esquema su representación geométrica es:

\csc \alpha = \overline{AG}

La secante: (abreviado como sec) es la razón inversa de coseno, o también su inverso multiplicativo:

\sec \alpha = \frac{1}{\cos \; \alpha} = \frac{c}{b}

En el esquema su representación geométrica es:

\sec \alpha = \overline{AD}

La Cotangente: (abreviado como cot o cta o ctg) es la razón inversa de la tangente, o también su inverso multiplicativo:

\cot \alpha = \frac{1}{\tan \alpha} = \frac{b}{a}

En el esquema su representación geométrica es:

\cot \alpha = \overline{GF}

Representación gráfica

Funciones trigonométricas recíprocas

Las funciones recíproca se denominan con el prefijo arco, cada razón trigonométrica posee su propia función recíproca:

$y= \sin \, x \,$

y es igual al seno de x, la función recíproca:

$x = \arcsin \; y \,$

x es el arco cuyo seno vale y, o también x es el arcoseno de y.

si:

$y= \cos x \,$

y es igual al coseno de x, la función recíproca:

$x = \arccos y \,$

x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.

si:

$y= \tan x \,$

y es igual al tangente de x, la función recíproca:

$x = \arctan y \,$

x es el arco cuya tangente vale y, o x es igual al arcotangente de y.

NOTA: Es común, que las funciones recíprocas sean escritas de esta manera:

$y = \operatorname {arcsin} \; x \quad \longrightarrow \quad y = \sin^{-1} x \,$

pero se debe tener cuidado de no confundirlas con:

$y = \cfrac{1}{\sin x} \quad \longrightarrow \quad y = \csc x$

Representación gráfica

EQUIVALENCIA ENTRE LAS FUNCIONES TRIGONOMÉTRICAS

	Seno	Coseno	Tangente	Cotangente	Secante	Cosecante
$\sin\theta\,$	$\sin\theta\,$	$\sqrt{1-\cos^{2}\theta}$	$\frac{\tan\theta}{\sqrt{1+\tan^{2}\theta}}$	$\frac{1}{\sqrt{1+\cot^{2}\theta}}$	$\frac{\sqrt{\sec^{2}\theta-1}}{\sec\theta}$	$\frac{1}{\csc\theta}$
$\cos\theta\,$	$\sqrt{1-\sin^{2}\theta}$	$\cos\theta\,$	$\frac{1}{\sqrt{1+\tan^{2}\theta}}$	$\frac{\cot\theta}{\sqrt{1+\cot^{2}\theta}}$	$\frac{1}{\sec\theta}$	$\frac{\sqrt{\csc^{2}\theta-1}}{\csc\theta}$
$\tan\theta\,$	$\frac{\sin\theta}{\sqrt{1-\sin^{2}\theta}}$	$\frac{\sqrt{1-\cos^{2}\theta}}{\cos\theta}$	$\tan\theta\,$	$\frac{1}{\cot\theta}$	$\sqrt{sec^{2}\theta-1}$	$\frac{1}{\sqrt{\csc^{2}\theta-1}}$
$\cot\theta\,$	$\frac{\sqrt{1-\sin^{2}\theta}}{\sin\theta}$	$\frac{\cos\theta}{\sqrt{1-\cos^{2}\theta}}$	$\frac{1}{\tan\theta}$	$\cot\theta\,$	$\frac{1}{\sqrt{\sec^{2}\theta-1}}$	$\sqrt{\csc^{2}\theta-1}$
$\sec\theta\,$	$\frac{1}{\sqrt{1-\sin^{2}\theta}}$	$\frac{1}{\cos\theta\,}$	$\sqrt{1+\tan^{2}\theta}$	$\frac{\sqrt{1+\cot^{2}\theta}}{\cot\theta}$	${\sec\theta}\,$	$\frac{\csc\theta}{\sqrt{\csc^{2}\theta-1}}$
$\csc\theta\,$	$\frac{1}{\sin\theta\,}$	$\frac{1}{\sqrt{1-\cos^{2}\theta}}$	$\frac{\sqrt{1+\tan^{2}\theta}}{\tan\theta}$	$\sqrt{1+\cot^{2}\theta}$	$\frac{\sec\theta}{\sqrt{\sec^{2}\theta-1}}$	${\csc\theta}\,$

VALOR DE LAS FUNCIONES TRIGONOMÉTRICAS


Circunferencia en radianes.	Circunferencia en grados sexagesimales.

Radianes	Grados sexagesimales	seno	coseno	tangente	cosecante	secante	cotangente
$0 \;$	$0^o \,$	$\frac{\sqrt{0}}{2}=0$	$\frac{\sqrt{4}}{2}=1$	$0 \,$	$\nexists (\pm \infty) \,\!$	$1 \,$	$\nexists (\pm \infty) \,\!$
$\frac{1}{6}\pi$	$30^o \,$	$\frac{\sqrt{1}}{2}=\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$	$2 \,$	$\frac{2}{\sqrt{3}}$	$\sqrt{3}$
$\frac{1}{4}\pi$	$45^o \,$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	$1 \,$	$\frac{2}{\sqrt{2}}$	$\frac{2}{\sqrt{2}}$	$1 \,$
$\frac{1}{3} \pi$	$60^o \,$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{1}}{2}=\frac{1}{2}$	$\sqrt{3}$	$\frac{2}{\sqrt{3}}$	$2 \,$	$\frac{1}{\sqrt{3}}$
$\frac{1}{2} \pi$	$90^o \,$	$\frac{\sqrt{4}}{2}=1$	$\frac{\sqrt{0}}{2}=0$	$\nexists (\pm \infty) \,\!$	$1 \,$	$\nexists (\pm \infty) \,\!$	$0 \,$